Miglioriamo insieme il mondo del risparmio gestito
Questo Blog ha lo scopo di alimentare un dibattito che ci auguriamo posso accrescere anche la nostra e la vostra cultura finanziaria, per colmare il gap che ci differenzia dal mondo anglosassone e per poi far prevalere la nostra creatività e genialità tipiche del popolo Italiano
- Dimensione carattere: Maggiore Minore
- Visite: 7420
- 13 Commenti - Inserisci il tuo
Paradosso di Monty Hall
Visto che questa settimana parto per una settimana di meritata (o quantomeno agognata...) vacanza, ho pensato di trattare un argomento leggero ma simpatico che vi farà comprendere che non sempre il mondo delle probabilità è lineare e comprensibile, e che spesso la realtà è contro-intuitiva, come avevo cercato di spiegare nel post Perchè i mercati sono controintuitivi.
Premetto che questo "gioco" ha scaldato l'opinione di migliaia di professori accademici e statistici, quindi sentitevi pure in diritto di pensare che il gioco che vi proporrò sembrerà sbagliato, ma abbiate il coraggio e l'umiltà di studiare il problema a fondo senza il pregiudizio di avere ragione e che il paradosso sia sbagliato (anche perché altrimenti non si chiamerebbe paradosso...).
Immaginate di essere protagonisti di un quiz televisivo, e vi viene proposto dal conduttore di scegliere una delle tre porte qui sopra rappresentate, dove dietro di esse si nascondono due capre ed una fiammante automobile nuova di zecca che se indovinerete dove si trova diventerà vostra.
La prima domanda è: quale probabilità avete di vincere l'automobile? risponderete ovviamente il 33,3%, ovvero un terzo delle possibilità
Ipotizzate di scegliere la porta di sinistra, a questo punto, il conduttore, che sa esattamente dove si trova l'automobile (e questo fattore è molto più determinante di quello che si pensa) apre la porta di centro, dove è certo che si trovi una delle due capre.
La seconda domanda è: che probabilità avete di vincere la macchina dopo che è stata aperta la porta da parte del conduttore televisivo? Molti diranno 50% perché sono rimaste due porte e questo, ma lo capirete dopo, è l'inganno che viene dalla nostra (sbagliata) percezione che abbiamo delle probabilità.
Ora il conducente vi propone di cambiare la propria scelta, visto che sapete dove si trova una capra, quindi in questo caso o di rimanere sulla porta di sinistra precedentemente scelta, oppure di scegliere quella di destra.
La terza domanda è: cambiano le probabilità di vittoria, cambiando la propria scelta?
Molti di voi diranno di no, poiché è intuitivo pensare che le probabilità siano al 50%, visto che sono due porte, ma come detto in apertura il paradosso è contro-intuitivo e quindi intuirete che vi sto per dire che invece le probabilità non solo cambiano ma addirittura raddoppiano.
Vi ricordate la prima domanda? la probabilità di vittoria iniziale era di un terzo, il fatto di avere aperto una porta non cambia la probabilità iniziale del 33,3%, semplicemente avete iniziato il percorso per scoprire se avevate avuto fortuna oppure no.
Viceversa, le altre due porte che non avete scelto possiedono ciascuna il 33,3% di vittoria, cumulativamente il 66,6% di vincere la macchina, concordate? quindi il fatto che il conduttore ne abbia aperta una vi da un vantaggio clamoroso, poiché le due porte insieme avevano il 66,6% di probabilità di avere dietro la macchina, ma avendone aperta una, il conducente vi sta offrendo su un piatto d'argento questa percentuale del 66,6%.
Quindi la risposta corretta è: cambiare la scelta fa raddoppiare le probabilità di vittoria.
A questo punto starete pensando: Daniele si è bevuto il cervello, la probabilità di vincere è il 50% e cambiare è irrilevante (soprattutto se non sono riuscito a trasmettervi bene il messaggio), oppure potrete dire, si ha ragione, ma senza esserne convinti o aver capito perché; in entrambi i casi vi invito a comprendere a fondo il problema con le due spiegazioni qui sotto e un video:
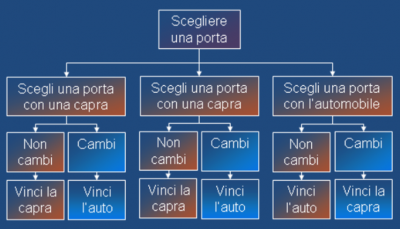
Questo diagramma di flusso, se lo analizzate fa capire che cambiare fa vincere l'auto 2 volte su 3, quindi il 66,6% delle volte, il che conferma quanto detto precedentemente.
Ecco il video tratto dalla serie televisiva Numb3rs:
ma per i più ostici ho pensato anche a questo esempio:
Immaginate che invece di tre porte ce ne siano 10; che probabilità avete di vincere una macchina invece di trovare una delle 9 capre? il 10% giusto; perfetto, ora scegliete una porta e il conduttore ne apre le altre 8 di cui sa per certo che dietro ci sono solo capre.
Rimangono aperte solo due porte, se inizialmente la probabilità da parte vostra di vincere era del 10%, le altre 9 porte possedevano cumulativamente il 90% di avere dietro l'auto; visto che il conduttore sa esattamente dove si trova l'auto (e come detto inizialmente questo fa la differenza) che probabilità ha l'unica porta rimasta chiusa oltre la vostra di avere dietro l'altra?
il 90% bravi! avete compreso il paradosso di Monty Hall, ora posso partire felice per le ferie!
Ci risentiamo ad agosto, sempre non vogliate commentare questo post (sempre gradito ricevere vostri commenti) oppure non desideriate condividerlo e aiutarci a diffondere a chi ritenete utile il nostro Blog.
Buone ferie a tutti
DB
Commenti
-
Sabato, 19 Luglio 2014Come al solito, oltre al contenuto scientifico che migliora la nostra comprensione delle dinamiche dei mercati, ci metti anche l'aspetto curioso e ludico che ci fa piacere di più il lato noioso della finanza.
Buone vacanze e se vieni a Bibione ti offro volentieri un drink!! -
Sabato, 19 Luglio 2014
Grazie David,
a Bibione quest'anno non credo di venire, se non per un week end.
eventualmente non mancherò.
buone ferie anche a te -
Lunedì, 21 Luglio 2014
Non conoscevo il paradosso. E' interessante....
Mi chiedo quante conoscenze potremmo aggiungere a quelle che abbiamo se avessimo tempo e curiosità?
Buone vacanze. -
Lunedì, 21 Luglio 2014
Caro Claudio,
più studi più sai di non sapere...
Quando ho scritto il mio primo paper e sono andato orgogliosamente a presentarlo alla conferenza FMA di Denver, mi sono trovato davanti ad una conferenza di tre giorni con 600 paper presentati in trenta sessioni parallele...
Ho capito che non avrei avuto mai il tempo e la forza di imparare tutto quello che riguarda un solo argomento specifico.
Però la cultura è l'unico bene al mondo che se condiviso aumenta la ricchezza dei partecipanti, quindi avanti tutti insieme per apprendere sempre cose nuove.
Se credi aiutaci a diffondere questo blog, a presto
DB -
Lunedì, 21 Luglio 2014
Il paradosso ha senso (e pertanto non è più un paradosso) proprio SE E SOLO SE il conduttore sa dove si trova l'automobile.
Se la scelta fosse puramente randomica tra le 10 porte, la probabilità finale sarebbe 50/50. Infatti è un errore da principianti considerare gli eventi statistici avere influenza uno con l'altro. L'evento 1 (10 porte) è separato dall'evento 8 (2 porte rimaste). La probabilità non si trasferisce magicamente da evento ad evento.
Ovviamente tutto cambia se inseriamo un conduttore che conosce quale sia la porta giusta. Ancora più forte è l'implicazione che egli apra tutte le porte dove sa non esserci l'auto. Se fosse il concorrente a scegliere quale aprire (quindi randomicamente), allora gli eventi sarebbero separati e non ci sarebbe nessun paradosso. -
Sabato, 09 Agosto 2014
Buongiorno Lapo,
non sono laureato né ho credenziali in campo matematico.
Detto questo non sono d'accordo con quanto lei scrive, ma potrei non aver compreso bene, né sono d'accordo con quanto sostenuto da S. Rosenthal nel suo articolo "Monty Hall, Monty Fall, Monty Crawl" in merito all'argomento "Il conduttore non sa cosa ci sia dietro le porte" che ho letto su Wikipedia.
La prima e la seconda scelta del giocatore non sono eventi separati, fanno entrambi parte dello stesso evento ed è possibile avvantaggiarsi sia nel caso che il conduttore conosca cosa è nascosto dietro ogni porta (Problema di Monty Hall) sia nel caso in cui il conduttore non ne sia a conoscenza (artico di S. Rosental)
E' chiaro che si può usufruire di un vantaggio solo se si arriva alla scelta finale e se all'inizio ho una scelta su tre, in altri casi i risultati cambiano.
Nel primo caso (il conduttore sa cosa c'è dietro le porte e mostra la porta con la capra) deciderò di cambiare la scelta iniziale.
Nel secondo caso (il conduttore non sa cosa nascondono le porte e aprendo la sua mostra una capra) deciderò di non cambiare la scelta iniziale.
Se qualcuno non è d'accordo proverò a spiegarlo... o se qualcuno vuol provare a farmi capire meglio ascolto volentieri..
Buone Vacanze Dottor Bernardi e Buone Vacanze a tutti quanti
Andrea R. -
Lunedì, 11 Agosto 2014
Buonasera Andrea,
Se il conduttore Sto arrivando! dove si trova l'auto, allora cambiando raddoppio le probabilità di vittoria, ovvero diventano 66,6% invece che 33,3%; questo significa che se gioco 100 volte e cambio sempre vincerò 66 automobili.
Se il conduttore non conosce dove è l'auto, ma se apre la porta e la trova mi fa vincere, indipendentemente dal fatto che io cambi o meno vincerò anche in questo caso 66 auto su 100 volte, questo perché si aprono due porte su tre ogni colta e quindi ho il 66,6% di probabilità di vincita, ma comunque in questo caso cambiare è ininfluente.
spero di essere stato sufficientemente chiaro.
buone vacanze anche a lei.
DB -
Sabato, 15 Novembre 2014
esatto..
-
Lunedì, 21 Luglio 2014
Corretto Lapo,
lo ho specificato due volte proprio perché la condizione è proprio quella, sarebbe quasi impossibile poter scegliere una nuova porta su 10 se il conduttore ne apre 8 a caso; l'80% delle volte il gioco finirebbe con il conduttore che trova l'auto dietro una porta...
Le venti volte su cento che ci si trovasse a scegliere allora ci sarebbe il 50% di probabilità, come hai correttamente specificato.
Aiutaci a diffondere il nostro Blog se credi, a presto
DB -
Lunedì, 21 Luglio 2014
Ma è fenomenale!!!
Quando ci propongono una scelta noi abbiamo la maggiore possibilità di scegliere quella sbagliata.
Cambiando invertiamo quella possibilità a nostro favore! -
Martedì, 12 Agosto 2014
...ah frequentisti!!! :
un bayesiano vedrebbe il tutto con occhi diversi! 
-
Sabato, 15 Novembre 2014
Caro Michele,
le probabilità condizionate sono basate proprio sul modello bayesiano...
Ti dico la verita: questo bellissimo paradosso mi era stato raccontato da mio figlio che l aveva studiato al liceo. E mi aveva chiaramente fregato.
Ottimo esempio per far capire che non tutto puo' risultare razionale come sembra...
Buone vacanze!!!